In der Welt der Mathematik treten wir häufig auf komplexe Probleme, die sowohl unsere Neugier als auch unsere Fähigkeiten zur Problemlösung in hohem Maße herausfordern. Der Wert von mathematischen Problemen und ihrer Komplexität kann jedoch nicht in ihrer Schwierigkeit allein gesehen werden. Es ist ihre Anwendung und ihr Auswirkungen auf andere Felder sowie ihr historischer Kontext und zukünftige Relevanz, die sie so fundamental wichtig machen. Dieses Stück wird einen umfassenden Überblick über die Definition komplexer mathematischer Probleme geben, die Methoden zu ihrer Lösung untersuchen und ihre Auswirkungen auf verschiedene Anwendungsfelder beleuchten. Darüber hinaus werden die historische Entwicklung dieser Probleme und die zukünftigen Trends in diesem faszinierenden Bereich der Mathematik dargestellt.

Definition komplexer mathematischer Probleme

Komplexe mathematische Probleme sind eine Unterklasse von mathematischen Aufgabenstellungen, die sich durch eine besondere Schwierigkeitsstufe und tiefgehende Konzepte hervorheben. Diese Aufgaben erfordern oftmals eine fortgeschrittene Kenntnis in mehreren Feldern der Mathematik und können vielfältige und vielschichtige Lösungswege beinhalten.

Mathematische Probleme sind allgegenwärtig – in der Physik, in der Ökonomie und sogar in den biologischen Wissenschaften. Sie helfen uns, die der Realität zugrundeliegenden Muster und Gesetzmäßigkeiten zu entziffern und neue wissenschaftliche Fortschritte zu erzielen. Komplexität in diesem Zusammenhang bezeichnet nicht unbedingt ein Problem, das schwer zu lösen ist, sondern vielmehr eines, das reich an Struktur und Detail ist.

Im spezifischen Kontext der Mathematik können komplexe Probleme mehrere Bereiche umfassen, von komplexen algebraischen Gleichungen und Ungleichungen über Funktionentheorie, Topologie und Geometrie bis hin zu kombinatorischer Mathematik und Wahrscheinlichkeitstheorie. Diese Komplexität kann sich in der Anzahl der beteiligten Variablen, der Anwendung fortschrittlicher Theorien, oder in der Art und Weise, wie verschiedene Konzepte und Prinzipien in einem Problem interagieren, widerspiegeln.

Komplexität ist meist ein Merkmal von Problemen, die neue Erkenntnisse oder Fortschritte in der Mathematik ermöglichen. Historisch gesehen haben komplexe Probleme oft zu bedeutenden Durchbrüchen geführt, wie der Lösung des Fermatschen letzten Satzes, der Entwicklung der Relativitätstheorie und der Quantenphysik und jüngst der Lösung des Poincaré-Vermuts.

Es ist wichtig zu notieren, dass obwohl komplexe mathematische Probleme oft anspruchsvoll sind, sie nicht unbedingt unbezwingbar sein müssen. Mit ausreichender Vorbereitung, fundiertem Wissen und festem Willen kann jeder Mathematiker Herausforderungen annehmen und letztlich die Lösungen für diese tiefgreifenden Probleme finden.

Deutlich ist, dass die Komplexität ein integraler Bestandteil der Mathematik ist und eine zentrale Rolle im Prozess der Kenntniserweiterung spielt. Es liegt in der Natur dieser Wissenschaft, fortwährend nach tiefgründigen und eingehenden Lösungen für komplexe Probleme zu suchen, um unsere Verständnis von der Welt kontinuierlich zu verbessern.

Methoden zur Lösung komplexer mathematischer Probleme

Um den komplexen Knoten mathematischer Probleme zu entwirren, müssen verschiedene Methoden angewendet werden. Diese Methoden können sich auf die Aspekte mathematischer Logik, Computer wissenschaftlicher Techniken und heuristischer Strategien stützen. Verstehen wir diese binnen Methoden besser, und somit den Angriff auf komplexe mathematische Probleme.

Mathematische Logik wird als unverzichtbares Werkzeug zur Lösung komplexer Probleme ingesamt betrachtet. Zum Beispiel kann die Rückwärtsarbeit, bei der Mathematiker von einem Problem zum anderen arbeiten und Schlüsse ziehen, einen klaren Weg zur Lösung bieten. Ebenso erlauben Beweismethoden, wie deduktive und induktive Argumentation, Mathematikern, Beziehungen zwischen verschiedenen Aspekten eines Problems zu erkennen und zu verifizieren, um zu einer Lösung zu gelangen.

Was die computerbasierten Lösungsmethoden angeht, sind Computer nicht nur Werkzeuge, sie haben auch die Art und Weise, wie mathematische Probleme gelöst werden, revolutioniert. Ein gutes Beispiel dafür sind Algorithmen, spezielle Rechenregeln und Operationsverfahren, die auf die Lösung spezifischer Problemtypen zugeschnitten sind. Diese selbst agierenden Prozesse können große Datenmengen verarbeiten und komplexe Berechnungen innerhalb kürzester Zeit durchführen.

Ein weiterer entscheidender Aspekt zur Lösung komplexer Probleme ist die Heuristik. Heuristiken sind Strategien, die dazu dienen, den Lösungsprozess zu beschleunigen, ohne dass eine Garantie für die beste oder genaueste Lösung besteht. Zum Beispiel kann die Verwendung von Näherungslösungen oder die Formulierung von Hypothesen helfen, schwierige mathematische Probleme zu lösen, indem sie eine allgemeine Richtung oder einen Lösungsansatz vorgeben.

Zusätzlich zu diesen Methoden müssen wir auch die Rolle der Zusammenarbeit in der modernen Mathematik anerkennen. Durch den Austausch von Ideen und die gegenseitige Herausforderung von Hypothesen können Mathematiker Wissen aufbauen und komplexe Probleme gemeinsam bewältigen. Ebenso hat die Bereitschaft, andere Disziplinen für neue Lösungsansätze heranzuziehen, die Breite und Tiefe der mathematischen Forschung erweitert.

Insgesamt gesehen, besteht kein universeller Weg, um komplexe mathematische Probleme zu lösen. Die Vielfalt und Flexibilität der Methoden reflektiert die Komplexität der Problemstellungen selbst. Es ist diese Komplexität, verbunden mit einem tiefen Verständnis und einer unaufhörlichen Leidenschaft für die Mathematik, die kontinuierlich zu Fortschritten in diesem umfassenden und faszinierenden Wissenschaftsgebiet führt. Doch trotz der Schwierigkeiten und Herausforderungen ist es genau dieser Prozess des Entdeckens, Erkennens und Verstehens, der den Reiz der Beschäftigung mit komplexen mathematischen Problemen ausmacht.

Auswirkungen komplexer mathematischer Probleme auf verschiedene Anwendungsfelder

Um komplexe mathematische Probleme zu knacken, bilden Rückwärtsarbeit und Beweismethoden nützliche Werkzeuge. Bei der Rückwärtsarbeit wird das Problem von der Lösung aus angegangen, um die dafür notwendigen Prozeduren zu erarbeiten. Beweise sind grundlegende mathematische Methoden, die eine Aussage mit restloser Sicherheit bestätigen oder widerlegen.

Mit der Cyberzeitalter wurde Computer zu unverzichtbaren Werkzeugen bei der Lösung mathematischer Probleme. Ihre rasend schnelle Rechenleistung und ihre Fähigkeit, große Datenmengen zu verarbeiten, haben dazu beigetragen, neue Gebiete der Mathematik zu erschließen, darunter die Kryptographie und die Algorithmik. Algorithmen sind spezielle Rechenregeln, die auf spezifische Problemtypen angewendet werden. Sie sind der Schlüssel zur Effizienz in Computerprogrammen und sie spielen eine kritische Rolle bei der Begrenzung der Komplexität.

Heuristik, eine Methode, die den Lösungsprozess durch ungefähre und intuitive Mittel beschleunigt, gibt den Unterschied zwischen einer Lösung in menschlicher Lebenszeit und Unbezwingbarkeit. Es ist wie das Navigieren in einem Labyrinth mittels einer groben Karte – nicht perfekt, aber oft ausreichend.

Trotz des Bildes des einzelnen Mathematikers als einsamen Problemlöser, ist die Zusammenarbeit und der Austausch von Ideen in der Mathematikgemeinschaft von unschätzbarem Wert. Hier können sich Ansätze, Methoden und Weltanschauungen austauschen, um neue Lösungsmöglichkeiten zu finden.

Die Vielfalt und Flexibilität der Methoden zur Lösung komplexer Probleme sind eine Inspiration für MathematikerInnen. Es gibt nicht die eine Methode, sondern viele Wege, die zum Ziel führen können. Dies fordert zur umfassenden Ausbildung und Diversifizierung der Kenntnisse und Fähigkeiten.

Die Leidenschaft für Mathematik entsteht häufig aus dem Reiz des Entdeckens. Es ist die Freude, ein unbekanntes Terrain zu erforschen und die Befriedigung, ein komplexes Problem geknackt zu haben. Komplexe mathematische Probleme bieten das fantastische Gefühl, an der Grenze des menschlichen Wissens zu arbeiten und diese mit jedem gelösten Problem ein Stückchen weiter zu schieben. Es ist eine Reise des Denkens, auf der man nie aufhört zu lernen und zu wachsen.

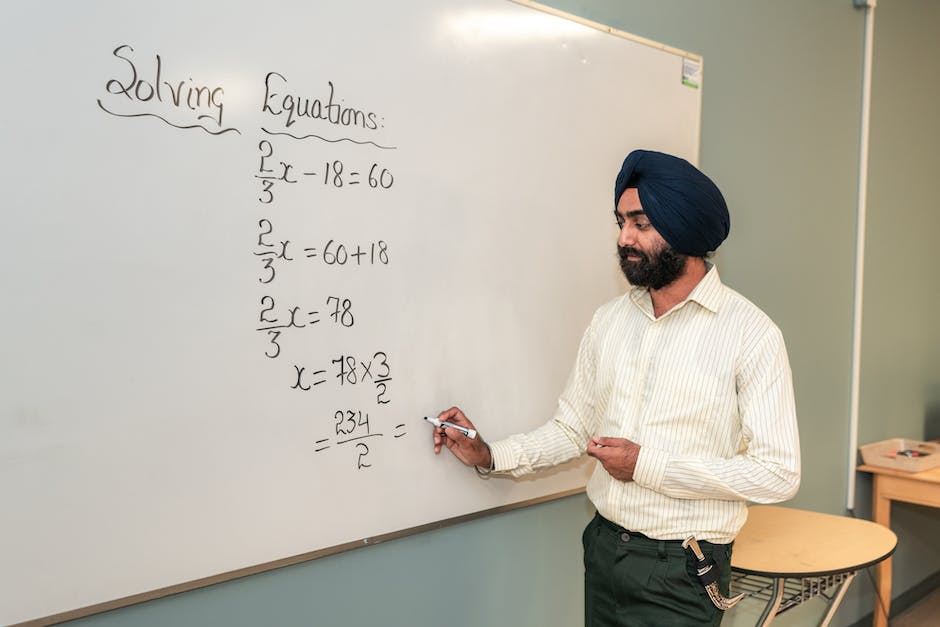
Historische Entwicklung und zukünftige Trends komplexer mathematischer Probleme

Die historische Entwicklung komplexer mathematischer Probleme ist eine faszinierende und inspirierende Geschichte. Es handelt sich um eine zeitlose Reise, die oft durch die Leidenschaft und Hingabe einzelner Denker vorangetrieben wurde. Mathematik hat nicht nur die Grundlage für unser Verständnis des Universums gelegt, sondern auch Technologien ermöglicht, die unser Leben auf beispiellose Weise verbessern.

Einer der entscheidenden Aspekte dieser historischen Entwicklung ist die zunehmende Vernetzung von Mathematik und Technologie. Computer wurden zu unverzichtbaren Werkzeugen für die Lösung komplexer Probleme und zur Durchführung komplizierter Berechnungen, die bisher nur imaginierbar waren. In unserem Datendurchdrungenen Zeitalter ist die Computer-Mathematik von entscheidender Bedeutung in der Kryptographie, der Bild- und Datenanalyse und der künstlichen Intelligenz.

Algorithmen haben einen enormen Einfluss auf unsere Welt. Ihre Ursprünge liegen in der Mathematik und sie spielen eine entscheidende Rolle, um komplexe Probleme effizient zu lösen. Es handelt sich um spezielle Berechnungsregeln, die darauf abzielen, effiziente Lösungsprozesse für spezifische Aufgaben bereitzustellen. Dank der Entwicklung von Algorithmen verwandeln wir umfangreiche und komplizierte Datenmengen in nützliche Informationen und schaffen damit neues Wissen.

Algorithmen und Computer haben jedoch ihre Grenzen. Heuristiken können dazu beitragen, diese Grenzen zu überwinden. Heuristiken sind Strategien, die zur Beschleunigung des Lösungsprozesses angewendet werden. Sie basieren auf der Konzentration auf die wahrscheinlichste Lösung, anstatt alle möglichen Lösungen zu durchforschen.

Die Zusammenarbeit und der Austausch von Ideen sind zentrale Elemente des Fortschritts der Mathematik. Wie die Geschichte zeigt, wurden viele bedeutende Durchbrüche durch die Zusammenarbeit von Wissenschaftlern erreicht. Es ist von entscheidender Bedeutung, dass Forscher aus der ganzen Welt weiterhin ihr Wissen und ihre Ideen miteinander teilen, um das kollektive Verständnis sowohl von spezialisierten als auch von interdisziplinären mathematischen Problemen zu vertiefen.

Die Lösung komplexer mathematischer Probleme erfordert vielfältige Methoden und Flexibilität. Die fachübergreifende Natur der Mathematik bietet zahlreiche Werkzeuge und Techniken für die Problemlösung, von abstrakten mathematischen Strukturen über spezielle Algorithmen bis hin zu fortschrittlichen Computerprogrammen.

Die Faszination, mathematische Muster zu entdecken und die Schönheit, die sich in komplexen Problemen verbirgt, treibt viele Mathematiker an. Diese Leidenschaft, gepaart mit der Freude am Lösen kniffliger Aufgaben, ist ein mächtiges Werkzeug, um das Unbekannte zu enträtseln und das Verständnis der Welt zu erweitern.

Blickt man in die Zukunft, so lässt sich der Trend zu einem stärkeren Fokus auf dem Gebiet der datengesteuerten Entscheidungsfindung und des maschinellen Lernens erkennen. Schon jetzt spielen komplexe mathematische Probleme eine zentrale Rolle in diesen Bereichen, und diese Rolle wird in den kommenden Jahren nur noch weiter zunehmen. Es ist zu erwarten, dass die zukünftigen Entwicklungen in der Mathematik sowohl unser Wissen über das Universum als auch unser tägliches Leben revolutionieren werden.

Die Lösung mathematischer Probleme ist nicht nur eine Herausforderung, sondern auch eine Möglichkeit, die menschliche Kreativität und das Streben nach Wissen zu fördern. Jedes gelöste Problem ist ein Schritt in Richtung Erweiterung unseres Verständnisses der Welt.

Die komplexe Welt der mathematischen Probleme ist reichhaltig und vielfältig, und ihre Erforschung hat weitreichende Auswirkungen auf unsere Welt. Von der Physik bis zur Wirtschaft bieten sie uns immer wieder neue Wege, wie wir die Welt verstehen. Das Studium ihrer historischen Entwicklung zeigt uns, wie weit wir in unserem Verständnis dieser Probleme gekommen sind, und wirft Licht auf die Möglichkeiten, die vor uns liegen. Man kann also sagen, dass die kontinuierliche Auseinandersetzung und Untersuchung dieser komplexen mathematischen Probleme entscheidend zur Entfaltung unseres Wissens und zur Ausgestaltung unserer Zukunft beiträgt.